- A+
摘要内容
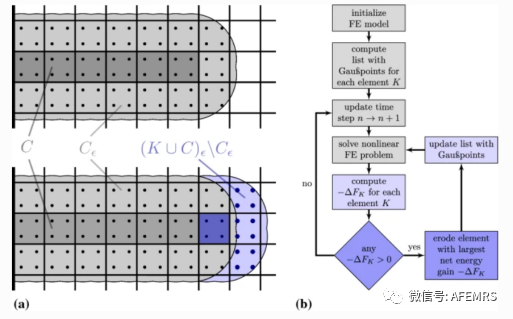
本文提出了在无尺度分离的情况下线性弹性动力学中桥接尺度的扩展/广义有限元方法。更准确地说,GFEM框架得到扩展,通过自动构建专门定制的形状函数,实现多尺度问题的数值求解,从而在简单、固定的有限元网格上实现高保真有限元建模。这在形状函数中引入了时间依赖性,因为它们会随着时间的不断调整而变化。通过考虑Newmark-β时间积分方案,研究了该公式的时间方面,并在显式时间步方案中探索了质量集总策略的有效性。该方法在典型波传播实例和动态断裂问题上进行了验证,以评估其准确性和灵活性。

摘要内容
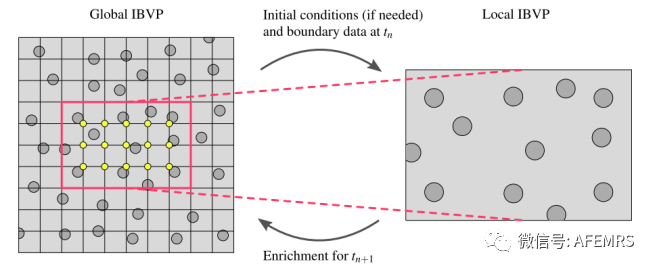
纤维网络断裂的计算分析是一个新兴的领域,应用于纸张、橡胶类材料、水凝胶、软生物组织和复合材料。光纤网络通常被描述为相互作用的一维元素的概率结构,例如桁架和梁。然后,可以将失效建模为位移场中的强不连续性,这些不连续性直接嵌入结构有限元中。至于其他应变软化材料,切刚度矩阵可以是非正定的,这降低了耦合(单片)双场问题解的鲁棒性。在本文中评估了交错与单片解方法,并评估了它们在纤维网络故障分析中的计算性能。本文提出了一种混合解决方案技术,可以优化计算分析的性能和鲁棒性。该技术在接近整体问题的切刚度矩阵时保留了正定元素刚度矩阵。该方法是通用的,还可以加速其他故障问题的计算分析。

摘要内容
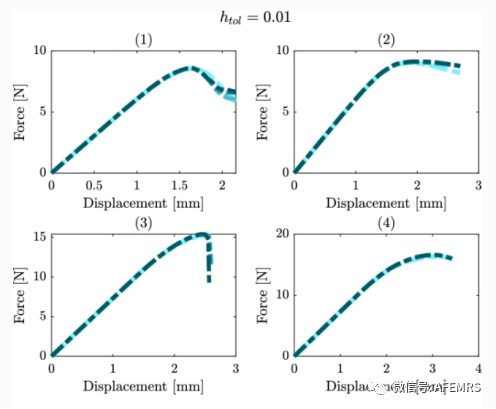
本文提出了一种通过非均质结构(例如金属微观结构)有效模拟延展性裂纹扩展的算法,其以体素数据的形式给出。该算法的基本思想是将有限单元法的优点与特征生成方法相结合,从而能够方便地将异构有限元问题与特征生成方法相结合,从而仍然能够实现与网格无关的裂纹扩展仿真。主要组成部分是从有限子单元切换到有限单元,从而通过将新出现的节点为悬挂节点来自动自适应地在裂纹尖端进行细化。与技术相关的裂纹在微尺度上的扩展问题主要与亚临界裂纹增长有关,其中裂纹随着随后的负载循环而快速和逐步移动。惯性变得很重要,这就是为什么通过将侵蚀元素的质量扩散到节点来考虑动力学,以避免侵蚀过程造成的质量损失。通过不同的三维数值算例对数值框架和体素分解技术进行了详细分析,验证了所提方法的有效性。