基于近场动力学-有限元耦合方法的正交各向异性多孔弹性介质中流体驱动压裂的数值模拟

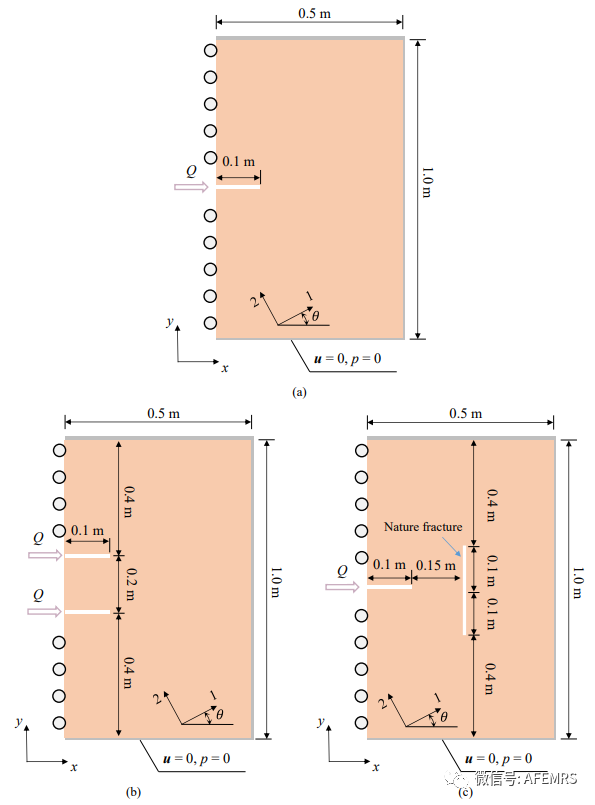
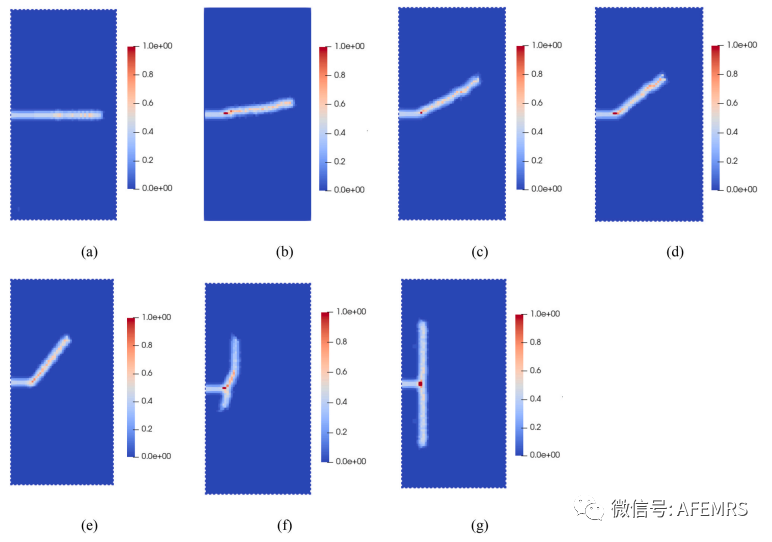
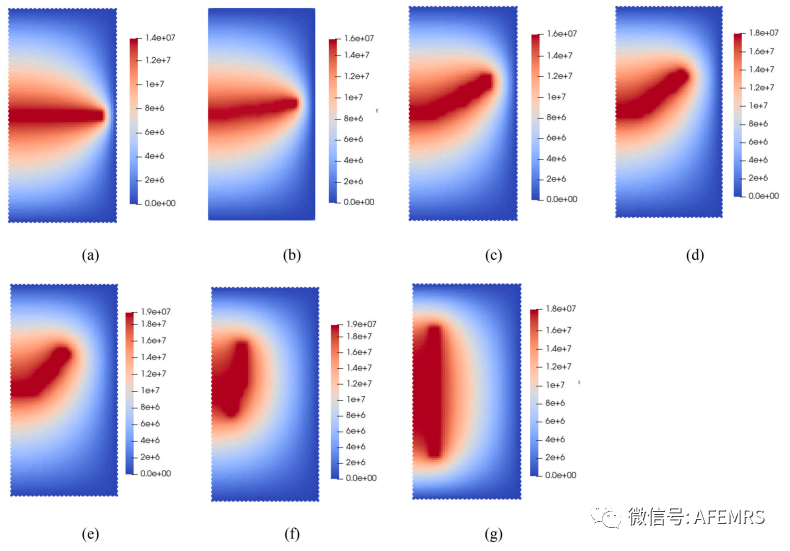
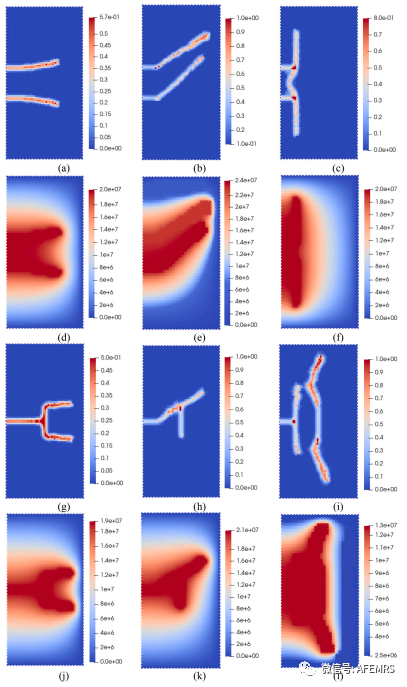
本文推广了近场动力学-有限元耦合方法来模拟正交各向异性多孔弹性介质中的流体驱动压裂。为此，本文提出了一个键微模量和临界能量密度随键取向连续变化的正交各向异性非普通态近场动力学( NOSBPD )模型。推导了包含用于捕捉固体裂缝的正交各向异性NOSBPD模型和用于模拟具有各向异性渗透张量的流体流动的有限元模型( FEM )的耦合系统的控制方程。为了确定所提出的正交各向异性NOSBPD模型合适的离散参数,进行了m -收敛和Δ-趋同研究。为了验证模型,模拟了不同材料取向的紧凑拉伸试验中的断裂扩展。弹性和渗透率各向异性、注入速度以及多裂缝和天然裂缝的存在对正交各向异性孔隙弹性介质中流体驱动的裂缝扩展有显著影响。在不同的材料角度下,断裂似乎偏离初始缺口方向,并且这种趋势随着弹性模量和垂直于弯曲平面的断裂释放率的降低而变得更加突出。渗透率各向异性影响流体模式和裂缝扩展长度。较快的注入速度导致更宽的损伤区和更弥散的孔隙压力场。