- A+

本文在前文的基础上,进一步深入研究。1882年,伟大的物理学家赫兹(就是后面通过试验证明了电磁波存在的那位)在研究光的干涉现象时,研究了透镜在相互接触力的作用下弹性变形会对干涉条纹造成影响,并发表了《论弹性固体的接触》一文,揭开了接触力学研究的序幕。
赫兹接触基于以下几个假设:
1、两接触面要至少二阶连续;
2、接触是非共形的;3、小变形(对于压入深度太大的时候需要进行修正);4、不考虑摩擦作用。
经典赫兹接触一般研究圆柱和球体等简单简单形状的接触,本文主要对两圆柱平行接触以及板-球接触分析。
一、两圆柱平行接触由于两个平行圆柱的接触可以进行简化,分别以平面应力、平面应变以及有限长度进行有限元分析。在相同网格的情况下(基于ansys),泊松比为0.3分别进行平面应力、平面应变分析,此时二者的接触应力分布如图1所示,可是二者的基础应力是有一些差别的,这主要与平面应变的接触应力计算与泊松比有关,而平面应力与接触应力无关。将泊松比改为0.1,重新计算平面应变,其接触应力如图2所示。


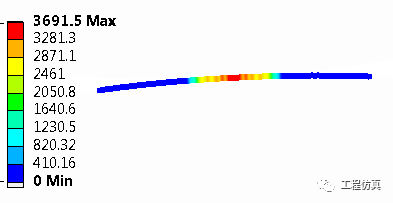
对于mises应力提取发现分别如图3、图4,发现泊松比0.3的情况下,平面应力状态下的mises应力位于接触点,而平面应变状态下的mises应力位于接触点下方,且数值是平面应力的远大于平面应变的,这与平面应变状态下有轴向方向应力,而平面应变在轴向方向的应力为0,造成了平面应变状态的mises应力与泊松比密切相关,且承受三向应力,因而其存在很高的静水压应力,从而其偏平面上的mises应力小于平面应力状态下的。修改泊松比为0.1,继续计算,如图4,其mises应力有所下降,且最大值位于接触点,区别于泊松比为0.3的位置。
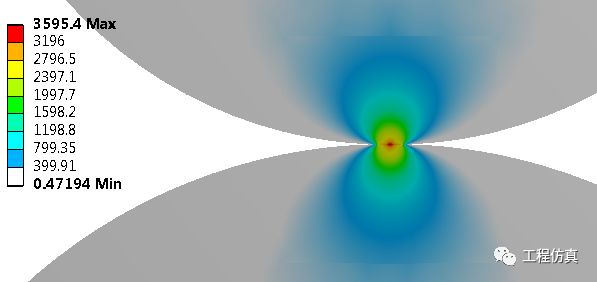

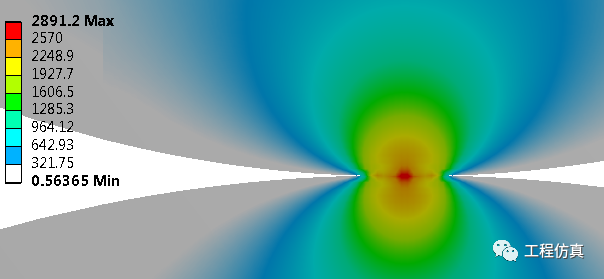
由于实际圆柱有一定长度,对有限长圆柱进行分析(泊松比0.3),见图5,结果发现接触应力在中部较大,两端较小,mises应力为两端较大,中间较小。可以认为中有限长圆柱的中部近似于平面应变状态,两端没有轴向方向应力,近似于平面应力状态。
图5 有限长圆柱分析二、,板-球接触分析采用轴对称模型分析,并设置泊松比为0.3(注意在ansys中对于2D的模型不可以定义线体为刚体模型,除了在显式动力学中,如图6),结果如图7,此时的最大mises应力位于接触点下方,理论上位于接触点下方的0.49a(a为接触半宽)处




