平面应变问题的维度转化

在符合平面应变简化条件的问题中, 由于要符合作用外力与纵向轴垂直，并且沿长度不变, 所以该问题在3D状态下, 必然不可能存在集中力, 载荷状态必然是分布式的, 所以载荷的主要形式有三种: 体积力, 面积力, 线积力.

    所以在该问题简化至平面应变问题的过程中, 只要研究这三种作用力的转变方式即可:

1. 三维空间中的体积力(例如重力)在二维空间中表现为面积力;
2. 三维空间中的面积力(例如压强, 面均布载荷)在二维空间中表现为线载荷(如线均布载荷),  需要将三维问题下的Pressure(N/mm2)降维至线均布载荷(N/mm);
3. 三维空间中的线载荷(如线均布载荷)在二维空间中表现为集中力, 也就是说在平面应变问题中求解得到的集中力(如支反力), 其实质上(三维空间中)是一个线均布载荷.

    第三点比较难于理解, 因为整个单位制和概念均发生了改变. 本文将通过实例计算的方式, 举例说明该如何进行换算.

01 符合平面应变条件的三维问题三维求解

模型如下:

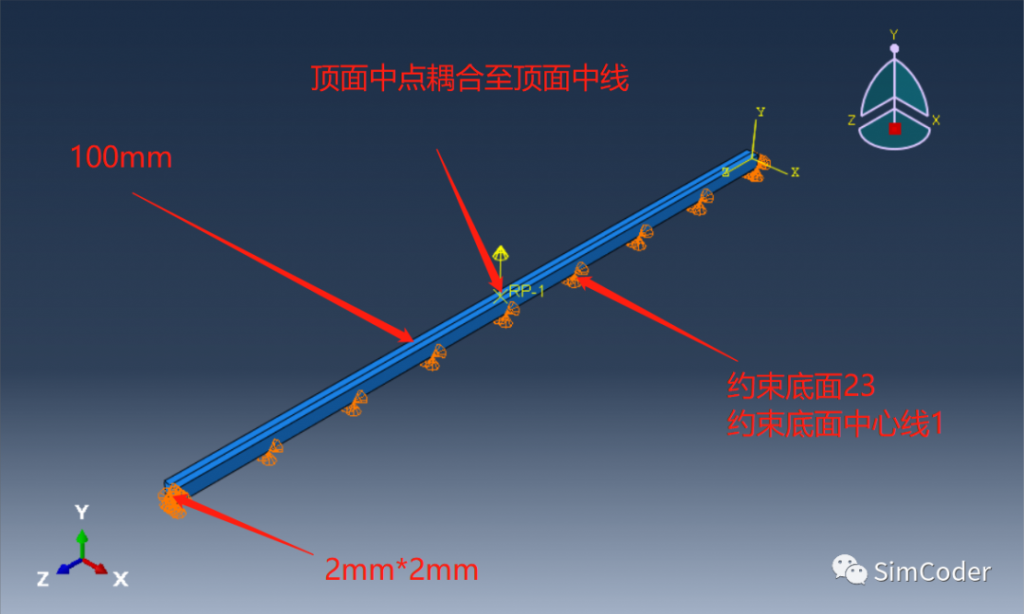
在参考点处施加1000N的作用力, 即相当于在顶面中心线施加了一个1000N/100mm=10N/mm的线均布载荷.

02 该问题的平面应变简化求解

模型简化如下:

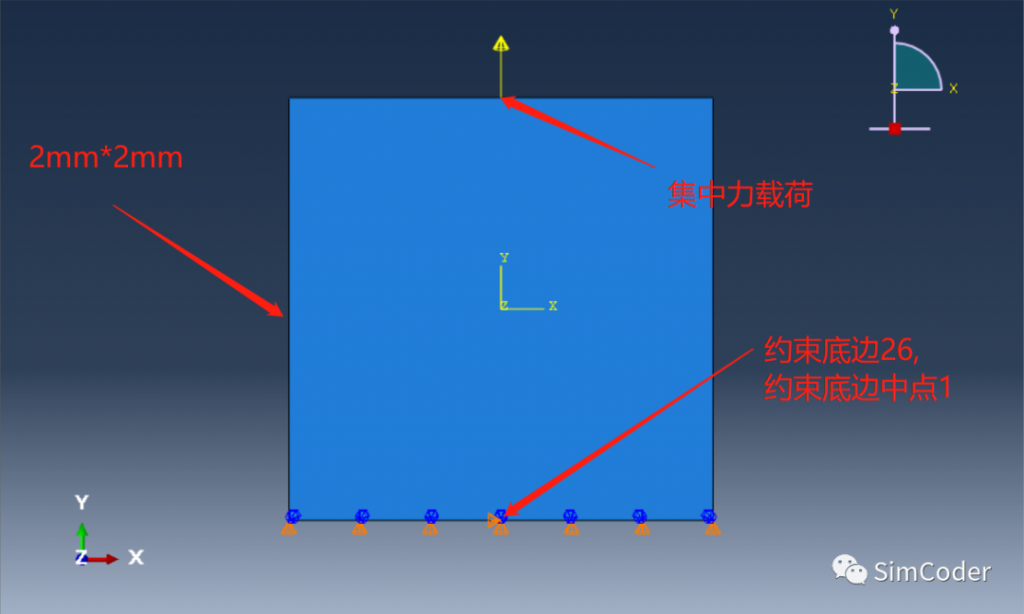
这样简化之后, 在顶边中点施加10N, 与三维求解中的线均布载荷数值相同, 用以确认彼此之间的转化方式.

03 分析结果对比

三维分析结果(取中间单元):

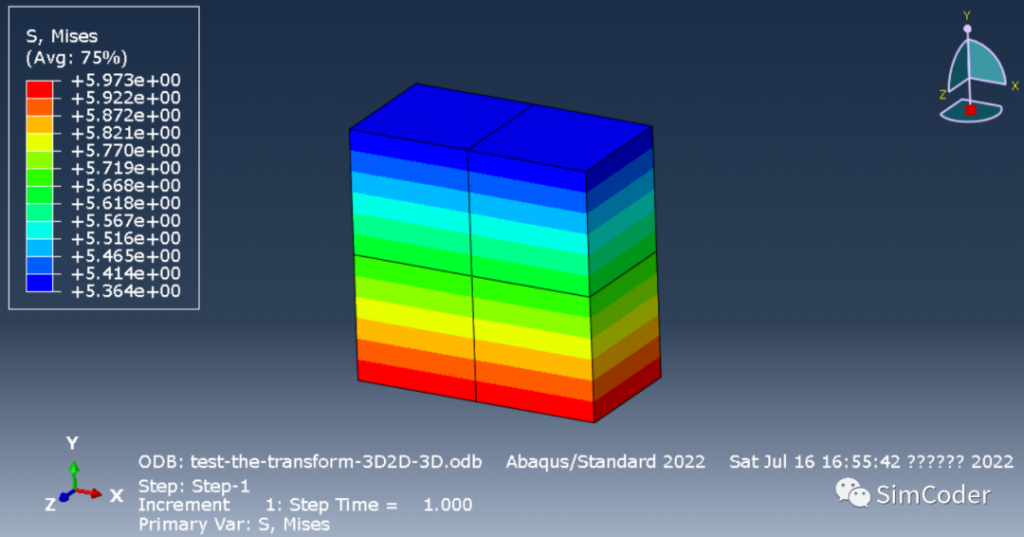
二维分析结果:

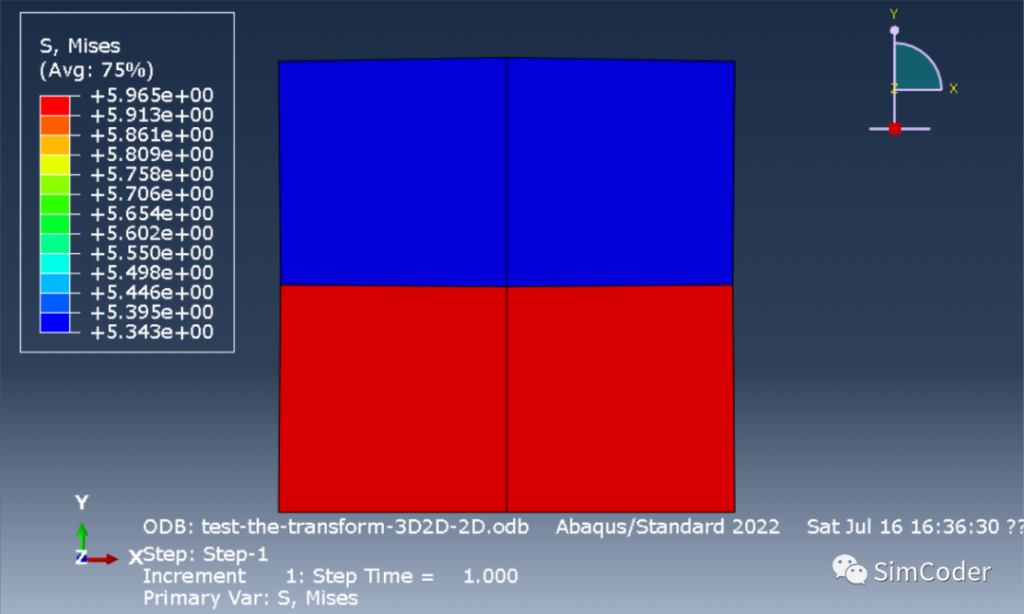
从求解结果可以看出两者的应力值基本相同, 其千分之几的误差应该是来自于两者的单元形函数的不同.

04 总结

通过这个简单的实例, 可以说明, 平面应变问题中, 在三维空间中的线均布载荷简化至二维空间中的时候会蜕变成一个点载荷, 同样的在二维空间中求解出来的点载荷的真实物理意义就是一个三维空间中的线均布载荷,通过此种方式可以获得载荷的总值.