薛定谔方程该写成什么样儿？

薛定谔方程  也不妨写成  的样子。薛定谔、彭罗斯、陈省身等在论及虚(复)数的诸多场合都是用的表示而非 “i”。i，-i是等价的，同时出现才能表达问题的完备性。

摘要 常见的薛定谔方程被写成的样子，将它写成的样子也未尝不可。其实，薛定谔1926年的推导是用±号的。考虑到波函数是复数，同时写出互为共轭的和才更准确，知道这一点有助于理解量子场论的正确形式。i，-i是方程x²=-1的根，它们是等价的，同时出现才能表达问题的完备性。采用的约定却不交代清楚背后的数学带来了很多误解。薛定谔1922年挽救外尔规范理论的论文，以及彭罗斯、陈省身等大数学家在论及虚 (复) 数的诸多场合都是用表示而非 “i”，这其中的道理值得我们深思。

2019年12月30日，我做出了我人生中一个大胆的举动，举办个人跨年演讲，演讲题目为“什么是量子力学”。在阐述量子力学就是由量子力学的那些方程所支撑起的理论这个观念时，我列举了量子力学的薛定谔方程 (1926)、泡利方程 (1927) 和狄拉克方程 (1928)，其中我把薛定谔方程写成了的形式。学过量子力学的朋友都知道，全世界的量子力学书中，近百年来薛定谔方程都是写成的样子的。这下完了，丢人丢大了，我把量子力学标志性的薛定谔方程给写错了。报告视频上传后，立马就有人指出这是个错误。

然而，哪儿不对劲儿。我第一次见到薛定谔方程是1984年秋，到2019年已有35年之久，此前我也翻译、讲授过薛定谔1926年的经典论文Quantisierung als Eigenwertproblem (量子化是本征值问题)，撰写过《量子力学少年版》，薛定谔方程对我来说应该是非常熟悉的存在。此前我都不知道写过多少遍了(虽然一直不懂。薛定谔从经典力学中构造出薛定谔方程的过程其实很难理解，那才是我们要学的大科学家的功夫)，怎么这次会写错呢？我翻了翻我自2012年以来的量子力学讲义和报告文件，发现也有几处就是写成了的样子的。这也不象是无心的输入错误啊？我似乎潜意识中一直想写。

2021年4月24日，为了撰写《磅礴为一》中的薛定谔一章，我读到彭罗斯 (Roger Penrose, 1931-) 在1996年给薛定谔的Nature and Greeks (自然与希腊人) 一书再版所写的序，其中有这样一段话：“Although these attempts had some success, the thrust of underlying mathematical conceptions has been, instead, to drive us in the direction of that curiously elegant form of continuity that is provided by complex numbers (numbers in which  features). Complex numbers are fundamental to quantum theory (and  occurs explicitly in Schrödinger’s equation)”， 联想起我为了撰写《云端脚下》还研习过的薛定谔1922年挽救规范场论的那篇论文，我恍然大悟将薛定谔方程写成的样子也是对的以及为什么我想这么写了。上述引的彭罗斯的第一句英文有点儿别扭，第二句倒是非常容易理解：“复数对于量子力学非常关键 (直白地出现在薛定谔方程里) ”。你注意没有，彭罗斯可不是说“i”直白地出现在薛定谔方程里。

有趣的是，我2007年就读过纸版的Nature and Greeks这本书，而且在上述这段话旁边还写下了“什么意思？”的批注 (图1)，可见那时候我就开始思考这个问题了。不过, 我已经完全忘了这茬儿了。唉！

那么，为什么薛定谔方程也可以写成的样子呢？或者说，光写 也有点儿不合适呢？容我慢慢分剖。

虚数是在研究一元三次方程的解法时不得已被引入的(参阅拙著《云端脚下》). 可解代数方程的解会表示成分圆方程xⁿ=1的n-个根的线性组合，对于一元二次方程，分圆方程x²=1有两个根，1，-1，故而一元二次方程的根公式为。你看，这里分圆方程x²=1的两个根是等价的、要同时被使用的，见于±1。上述公式与完备性、数域的封闭性有关，也很哲学 (用待求的解表示解)。请记住这一点。

解代数方程时会遭遇方程x²=-1的问题，这个方程有两个根，记为i，-i。引入了i，-i以后，代数方程的解若有根z=a+ib，也必有根z=a-ib，这就是所谓的代数定理。你看，i，-i必须同时出现。记复数z=x+iy，则必然要有伴随的，称为互为共轭的。在Wirtinger 导数中，和也要同时出现。作为纯虚数， i，-i是等价的；构成复数 (二元数)，z=x+iy和是共轭的。复数及其复共轭一起出现才是完备的。这一点在摆弄薛定谔方程的波函数 (是复数) 时似乎不必太在意，但在量子场论中就得注意了。

等价、对称要针对具体的语境。分圆方程x²=1有两个根，1，-1，它们是等价的，构成群。单靠i，-i不能构成群。但是i，-i 和1，-1 一起构成分圆方程x⁴=1的四个根，它们一起构成一个群。在这个语境下，1，-1，i，-i四者是等价的。

研究复数和复变函数一般就拿z=x+iy说事儿，这让很多人忘了也是必须同时出现的。记是一个不完备的选择， 也成立。如果大家足够细心，很会发现很多场合下数理大家们，如本文提及的薛定谔、彭罗斯与陈省身，是选择的写法而不是草率地写下 “i” (图2)。

薛定谔1922年论文与挽救外尔理论的第一步

1918年5月，外尔 (Hermann Weyl, 1885-1955) 发表了一篇题为“Gravitation und Elektrizität (引力与电) ”的论文，试图统一引力和电磁理论，这后来成了规范场论的第一篇论文。在这篇文章中，外尔得到了一个结论，电磁场存在的时空里时空距离的平行移动会为时空长度带来一个变换因子 。爱因斯坦 (他推荐的这篇论文) 在这篇论文之后有个评论：“Wäre dies in der Natur wirklich so, dann könnte es nicht chemisch Elemente mit Spektrallinien von bestimmter Frequenz geben, sondern es müsste die relative Frequenz zweier (räumlich benachbarter) Atome der gleichen Art im allgemeinen verschieden sein. Da dies nicht der Fall ist, scheint mir die Grundhypothese der Theorie leider nicht annehmbar, deren Tiefe und Kühnheit aber jeden Leser mit Bewunderung erfüllen muss (如果自然真是这样的，则不可能存在具有确定频率之谱线的化学元素，而是空间上相近的两个同种原子一般来说会有不同的相关频率。既然事情不是这样的，这个理论的基本假设在我看来就是不可接受的。当然啦，这个理论的深度与胆识每个读者都会佩服的) ”。外尔虽然稍微作了几句辩护，但爱因斯坦的挑剔确实指出了问题的症结。这篇文章发表后的一段时间里没有后续进展。它在等着薛定谔1922年和1926年的两篇突破性论文来救它。

1922年，薛定谔发表了题为“关于单电子量子轨道的一个值得注意的特性 (Über eine bemerkenswerte Eigenschaft der Quantenbahnen eines einzelnen Elektrons) 的论文，建议将外尔的时空长度变换因子中的γ定义为，这可以说是挽救外尔理论的第一步。在论文中，薛定谔指出，那个能得到 (氢原子) 能量谱的量子化条件，，其中是系统在一个周期内的平均动能，可以使得中的指数对于系统的一个周期积分是的整数倍。将量子化条件用到中的积分项上，可得出个近似结果   。如果电子沿轨道的运动带来 “长度”的变化，每个周期过后时空有“长度”变化  ，薛定谔说他很难相信这是量子化条件的偶然数学结果而没有深刻的物理意义。注意到有两个量纲为作用量的物理常数，一个是普朗克常数h， 一个是，于是薛定谔选择假设 ， 则那个变化因子变成了模为1的复数，就能有效避免所谓的电子运动带来的“长度”变化了。

笔者愿意强调，这是薛定谔挽救外尔理论——即后来的规范场论——的第一步，用的是量子化条件。

4

薛定谔1926年的论文与挽救外尔理论的第二步

1926年，薛定谔分四部分发表了Quantisierung als Eigenwertproblem一文，这是量子力学之波动力学形式的奠基性文章。请注意，薛定谔的这篇发表在Annalen der Physik 杂志上的论文整整140页！140页！140页！不知道几个学过量子力学的朋友知道这一点——关于量子力学诞生历史的描述给我们的印象是薛定谔几笔就划拉出来了一个方程，那篇论文估计也就是三五页的长度。笔者以为，这篇文章的题目“量子化作为本征值问题”，同黎曼1859年引Quanta这个词入 (复) 几何学以及用虚 (复) 数表示的量子化条件 (玻恩的手笔)，这三者才是量子力学的精髓。一般量子力学教科书根本是不明就里，基本上就是在那里解二阶微分方程而已。当然，解方程也分懂不懂物理，Friedrich Hund 解薛定谔方程就解出了量子隧穿的概念。

令笔者万分惊奇的是，那个量子力学的标志性方程，即后来被称为薛定谔方程的方程， 第一次出现是在该论文的第四部分，即全文总140页的第113页上 (图3) ！而且你看到方程里用的是 ±号！±号！±号！这就是说，把薛定谔方程写成 或者  的样子都对。实际上，在该论文总第134页上， 薛定谔引入关于时间、空间坐标微分的算符时也是都带±号的 (图4)。用方程  替代方程  ，对应的是变换t→-t或者把关系式   改写成，不会带来物理问题的差别。当然了，正确的做法是分别用于波函数和它的共轭上，这一点薛定谔当时就是这样处理的 (图5)。再重复一遍，对于薛定谔方程这一点也许不重要 (对时间只有一阶微分)，在量子场论里波函数和波函数的共轭应是同时出现的。

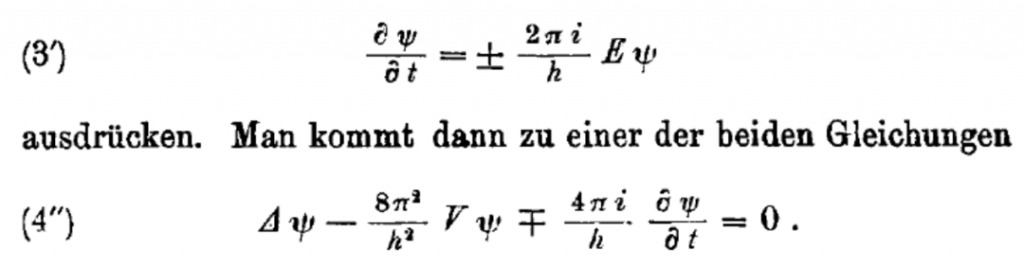
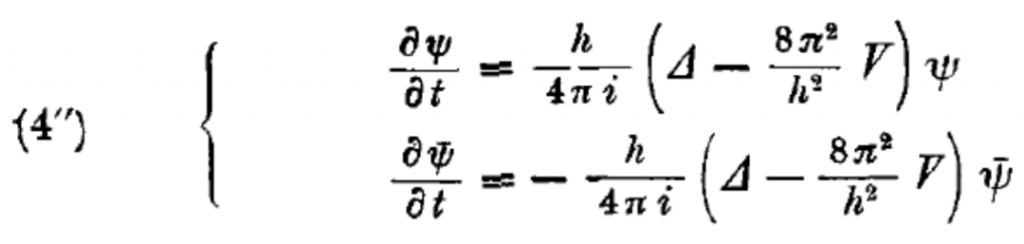
有了薛定谔方程的量子力学进入了新时代。1927年V.Fock和F. London 把薛定谔波动方程中的波函数变换同电磁规范变换结合在一起，从而带来了外尔理论的复活。1929年，外尔重新回到他1918年思考的问题，发表了“Elektron und Gravitation (电子与引力)”一文，其中给规范变换补上了波函数变换，这标志着规范场论的正式诞生。此处不展开讨论。

至此我算是说清楚了把薛定谔方程写成  或者 的样子皆可。其实，是将共轭的形式都写出来更好。然而，一个具有物理学史的问题又来了。在薛定谔1926年的经典论文里，并没有出现方程 。Hamilton一词在薛定谔1926论文中出现16次，但涉及的都是哈密顿的经典力学理论。谁、何时把方程写成了 的形式的，谁把这个方程叫成了薛定谔方程的 (总不会是薛定谔自己吧) ？薛定谔1926年谈论矩阵力学同他的波动力学等价的论文中，方程形式为  也不是  的样子， 见图6。笔者发现，在玻恩1926年6月25日递交的论文 Zur Quantenmechanik der Stossvorgänge (论碰撞过程的量子力学) 中，就有die Schrödingersche Wellengleichung (薛定谔波方程) 、der Schrödingerschen  Differentialgleichung (薛定谔微分方程) 的说法了，但却没有方程的影子。或许Mehra的the historical development of quantum theory中有线索，有空了俺再找找。

直说吧。其一，练拳不练功，到老一场空。数学就是物理人的根基功夫。薛定谔的数学跟克莱因、外尔当然不能比，但似乎比爱因斯坦要强一些，在真一流物理学家中是靠前的。其1922年引入，，这带来了这个理论中数系的扩展，这是规范场论这样的理论之威力的源泉。重要的意义在于这么做了以后，他1926年引入 (复) 波函数以及别人为电磁规范变换加上波函数变换就没有任何心理上的困难了。薛定谔本人一直思考统一场论方向的问题，这也是他和爱因斯坦、外尔可为伯仲的地方，他的《时空结构》一书表明他是相对论、统一场论方向的一流学者。有趣的是，薛定谔自己引入的，构造了波动力学的薛定谔方程引入了波函数，但是挽救或者说促成了规范场论的却不是他，临门一脚归了两位年轻人V. Fock和F. London。也许是波动力学的成功喜悦太冲了吧！

感慨之二是我稀里糊涂交错地写了几年的  和  也浑然不知。我在浏览过薛定谔1922和1926年的论文，在撰写《云端脚下》一书时仔细研究过复数的意义以及规范场论的基础， 期间和 ，以及共轭、完备性、封闭性啊这些概念不知道在我面前晃过多少次，我仍然是浑然不觉。直到2021年04月24日重读彭罗斯为薛定谔写的序，那个才变得生动、清晰起来。打开一本书最迷人的地方，是你不知道那里的哪一句话会为你打开一扇意想不到的门！时常，这样的一句话可能早在你面前晃荡到疲倦了。唉，郁闷，不说啦。