基于有限元的参数化偏微分方程深度学习求解器

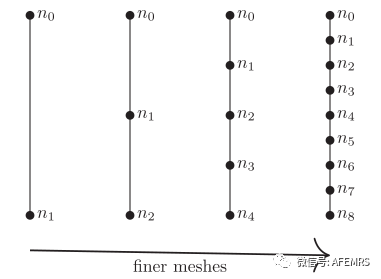
我们介绍了一种基于有限元法（FEM）求解线性参数偏微分方程（PDE）的动态深度学习（DL）体系结构。在进行网格细化时，用架构中神经元之间的连接模拟有限元连接。文中使用预条件和不同的范数来选择和讨论几种损失，以增强收敛性。为了简单起见，本文在一个空间域（1D）中实现了生成的Deep FEM。虽然使用Deep FEM解决非参数问题的计算效率很低，但解决参数问题时的执行时间与非参数问题相当（即所用迭代次数相似），这是该方法的真正威力所在。大量的数值实验表明，对于参数和非参数问题中的对称正定（SPD）和不定问题，通常都有很好的近似性。