比例边界有限元法中高阶形状函数的再探讨

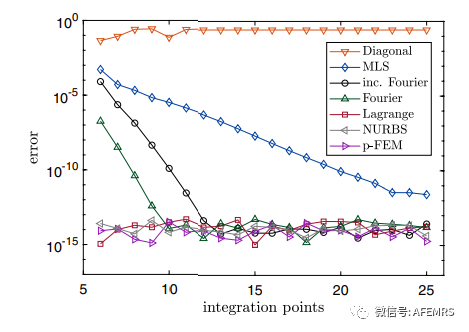
比例边界有限元法（SBFEM）是一种求解偏微分方程的半解析方法，其中对区域边界采用有限元近似方法，同时寻求解析解来描述区域内部的解。自SBFEM提出以来，已经应用了许多不同的形函数来插值边界上的解。本文在SBFEM的背景下，审查可用插值函数的各自优缺点，并就其应用提出建议。此外，我们详细讨论了所谓的对角SBFEM中使用的离散化。

在本文对最优形函数的探讨中，分别采用高阶傅里叶形函数、高阶NURBS形函数与传统的低阶形函数以及拉格朗日形函数进行对比，并从理论和数值实验两个角度探讨以上几种方案的优劣与在不同情况下的取舍。