二维和三维线弹性断裂力学的简单、一阶、条件良好且最优收敛的广义扩展有限元

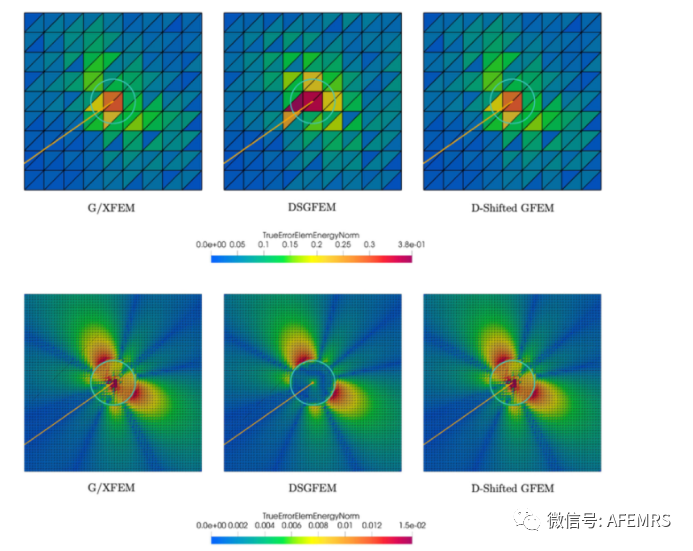
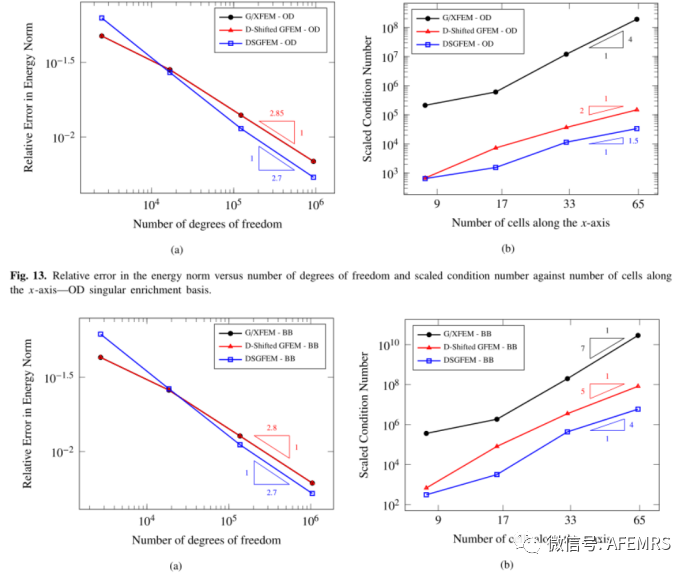
本文针对二维和三维线弹性断裂力学问题，提出了一种一阶广义扩展有限元法（GXEM）。该方法的条件处理顺序与标准FEM相同，并且对于网格相对于二维或三维裂缝的位置而言，它是稳健的。即使断裂前沿附近的问题的解不包含在所采用的奇异丰度所跨越的空间中，该方法也能在能量范数下达到最佳收敛速度。通过将其节点值与对角线预调节器相结合进行移位，实现了对与Heaviside富集函数相关的调节的控制。在奇异富集函数的情况下，采用了富集移位概念的简单扩展，表示为间断移位。这些修改是保留空间的，修改的浓缩跨越的解空间与未修改的浓缩横跨的解空间相同。文献中提出的调节控制策略通常不是这种情况。这些浓缩修改的计算成本可以忽略不计，并且在现有G/XFEM软件中的实现非常简单。借助典型的二维和三维问题，包括非平面裂缝和弯曲裂缝前缘的情况，数值说明了该方法的最佳收敛性、良好条件和鲁棒性。